As Redes Neurais Convolucionais (ConvNet ou CNN) são um tipo especializado de algoritmo de aprendizado profundo, projetado para tarefas que exigem reconhecimento de objetos (como classificação, detecção e segmentação de imagens).
Saiba a diferença entre classificação, detecção e segmentação de imagens no link a seguir
De forma geral, o que uma ConvNet faz é ler uma imagem de entrada, extrair características (pesos e vieses que podem ser aprendidos) e, assim, fazê-la se diferenciar de outros tipos de imagens.
Por exemplo, se eu tenho a imagem de uma bicicleta e quero fazê-la se diferenciar de qualquer outra imagem que não seja uma bicicleta, preciso extrair as características principais da bicicleta que a diferenciam de qualquer outra coisa.
Para nós humanos, basta verificar características como:
- pedais;
- corrente;
- guidão;
- selim;
- rodas.
Contudo, motocicletas também apresentam as mesmas características, sendo necessárias descrições mais claras e específicas para distinguir ambos os meios de locomoção.
Da mesma forma, as CNNs precisam captar o máximo possível da imagem de entrada. Isso envolve verificar cada pixel fornecido, realizar várias etapas de transformação e ir captando, em cada camada, características mais precisas.
As CNNs são divididas em camadas, sendo elas:
- Camada Convolucional (Convolution Layer)
- Camada de Pooling (Pooling Layer)
- Camada Totalmente conectada (Fully Connected Layer)
Então elas filtram linhas, curvas e bordas das imagens e, em cada camada acrescida, transformam essa imagem em uma imagem mais complexa.
A figura abaixo ilustra bem esse processo, que será explicado em detalhes a seguir.
 |
| https://learnopencv.com/understanding-convolutional-neural-networks-cnn/ |
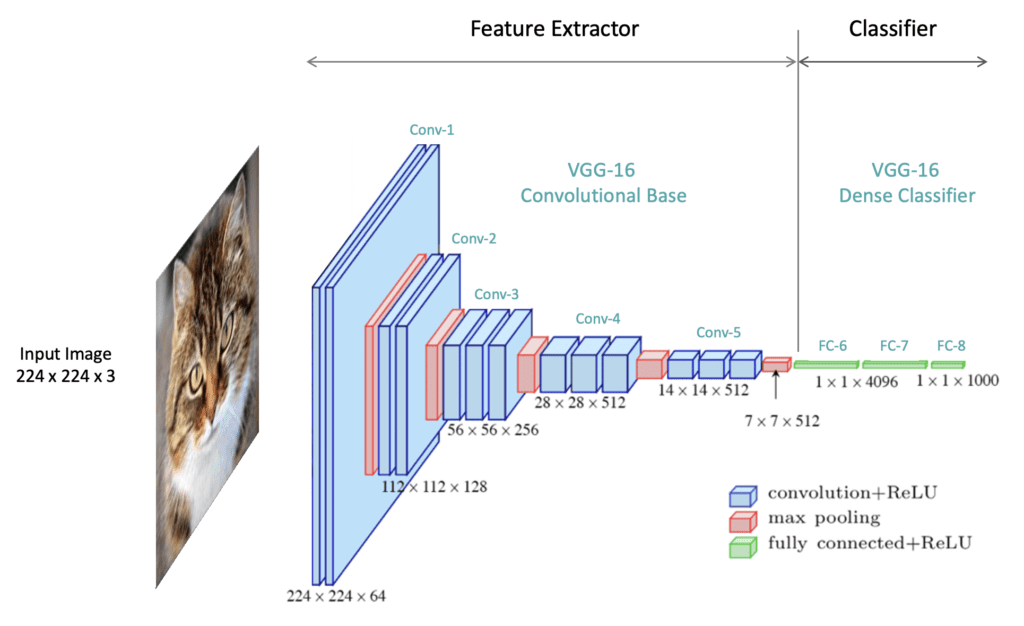
Entrada
A entrada é uma imagem de três dimensões, sendo elas altura, largura e profundidade.
A profundidade é normalmente definida pela quantidade de canais de cores. O RGB, um filtro com três canais, é o mais usado.
E aqui vale explicar a diferença entre canal, filtro e kernel.
Filtro corresponde a um conjunto de canais; um canal também pode ser chamado de kernel.
 |
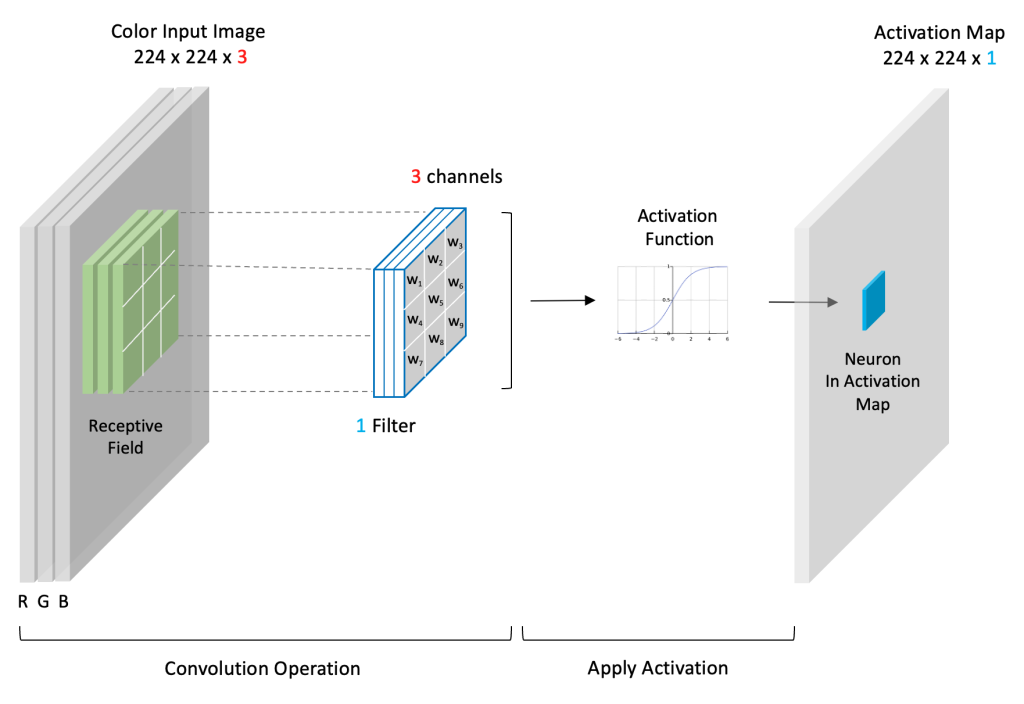
| Uma imagem de entrada com 1 filtro de 3 canais (RGB) e largura e altura de 4 pixels |
Camada Convolucional
A camada convolucional serve para extrair as características variadas das imagens. Vale destacar que uma camada convolucional pode ter mais de uma convolução.
Cada convolução é representada por um filtro (ou kernel) que vê pequenos quadrados e vai passando por toda a imagem capturando as características.
É importante frisar que esse kernel (ou filtro) do qual falo agora não é o mesmo que o da entrada. Na camada convolucional, kernel (ou filtro) se refere às configurações que buscam realçar alguma característica da imagem e criar, assim, um mapa de ativação ou de características.
Essas configurações são formadas inicialmente por pesos aleatórios, atualizados a cada nova entrada durante o processo de backpropagation.
Para entender o funcionamento da convolução, observe a imagem.
Inicialmente temos uma entrada de dimensões 6x6 e um kernel de dimensões 3x3. Vamos desconsiderar a profundidade da entrada nesse exemplo.
A primeira etapa da convolução é definir os seus hiperparâmetros.
Os hiperparâmetros são:
- stride = é o passo que o kernel dará pela imagem de entrada. Quanto maior o stride, menor a imagem de saída (feature map).
- padding = número de pixels adicionados à imagem de entrada quando ela está sendo processada pelo kernel. Seu objetivo é preservar o tamanho da imagem.
No nosso caso, mantemos stride = 1 e padding = 0. Isso significa que o tamanho da imagem de saída não manterá o tamanho da imagem de entrada (padding), porém não será muito reduzida (stride = 1).
A segunda etapa é posicionar o receptive field no início da imagem, para assim começar a passar o kernel por ela, varrendo-a por completo. Receptive Field refere-se à pequena região da entrada onde o filtro é aplicado.
A cada passada do kernel, o cálculo da soma das multiplicações de cada pixel da imagem pelo pixel do kernel é realizado e o resultado é salvo na matriz de saída.
O tamanho da matriz de saída é dado pela seguinte equação: 
, onde i = imagem de entrada, f = filtro (kernel), p = padding e s = stride.
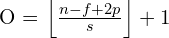
, onde i = imagem de entrada, f = filtro (kernel), p = padding e s = stride.Aplicando a fórmula nesse exemplo, temos que [(6 - 3 + 2.0)/1] + 1 = 4. Logo, as dimensões da matriz de saída é 4x4.
A profundidade da saída de uma convolução é igual à quantidade de filtros aplicados. Quanto mais profundas são as camadas das convoluções, mais detalhados são os traços identificados no activation (feature) map.
Uma pergunta que pode surgir (e que eu mesma tive essa dúvida) é: então a profundidade do RGB (1 filtro de 3 canais) vai gerar 3 mapas de características?
A resposta é não! Na verdade, o que gera mapas de características são os kernels da convolução. Se tiverem 2 kernels, então serão dois feature maps, sendo essa a profundidade da saída de que falei um pouco antes.
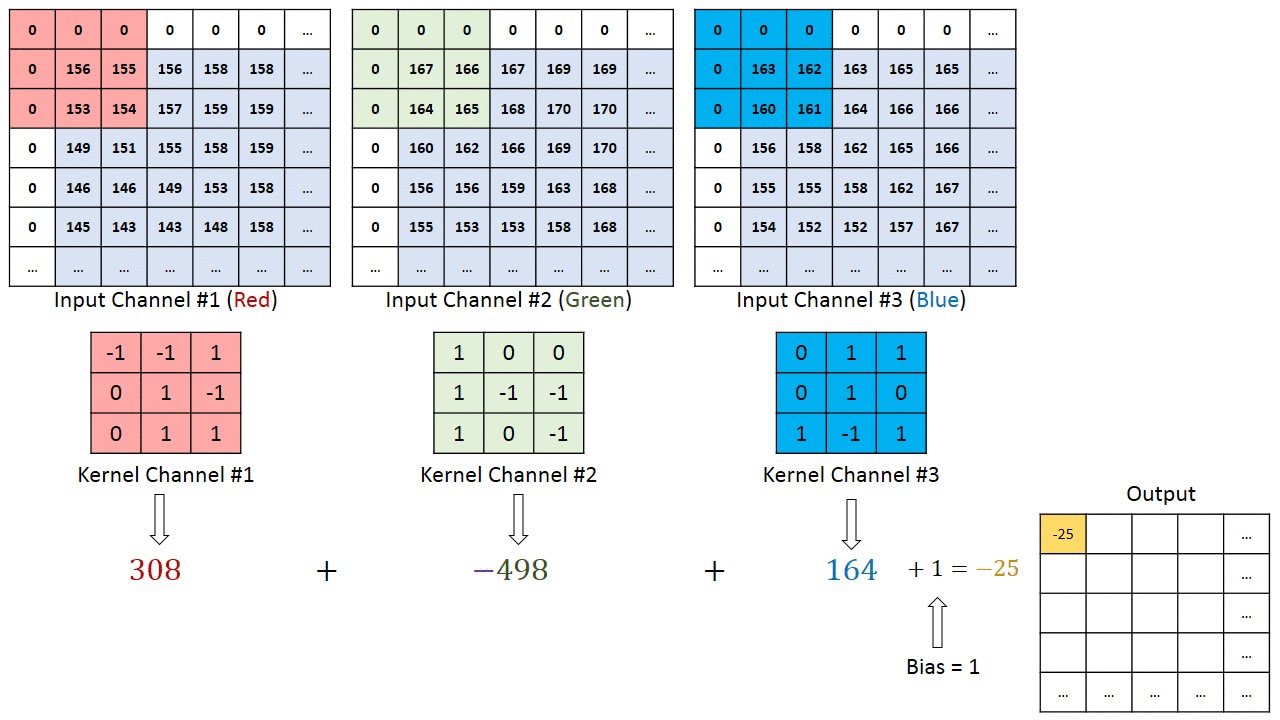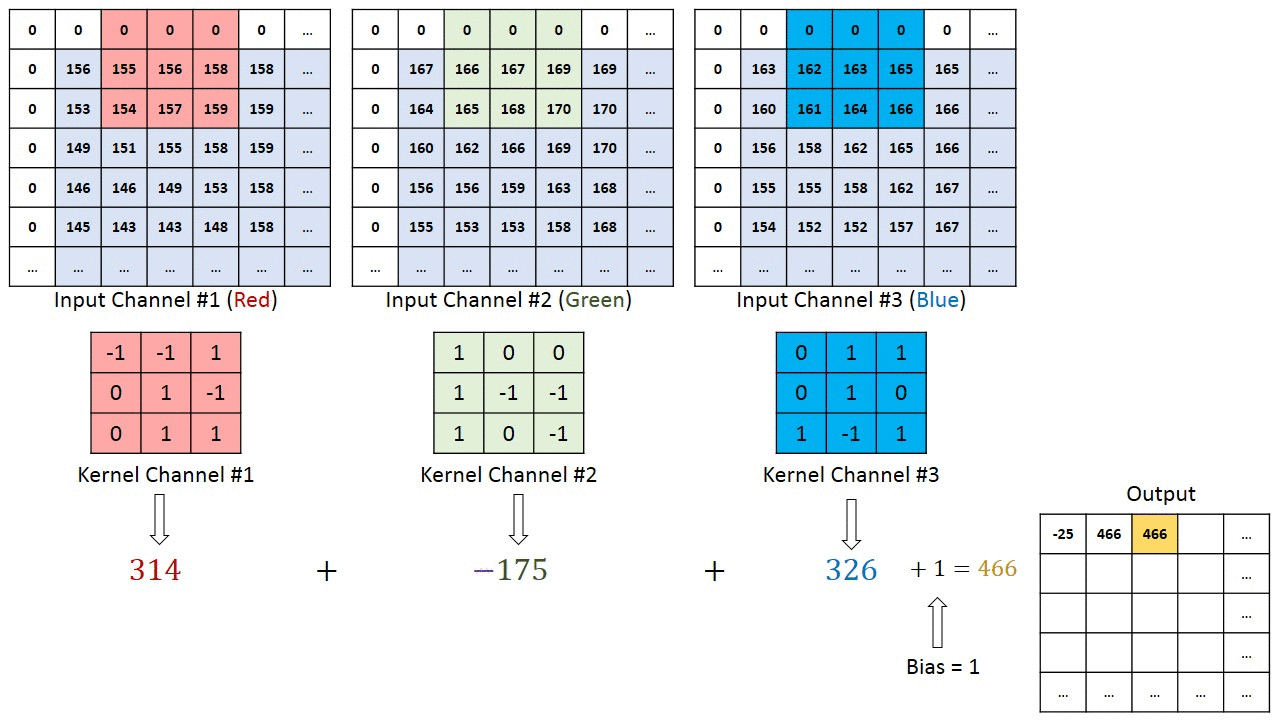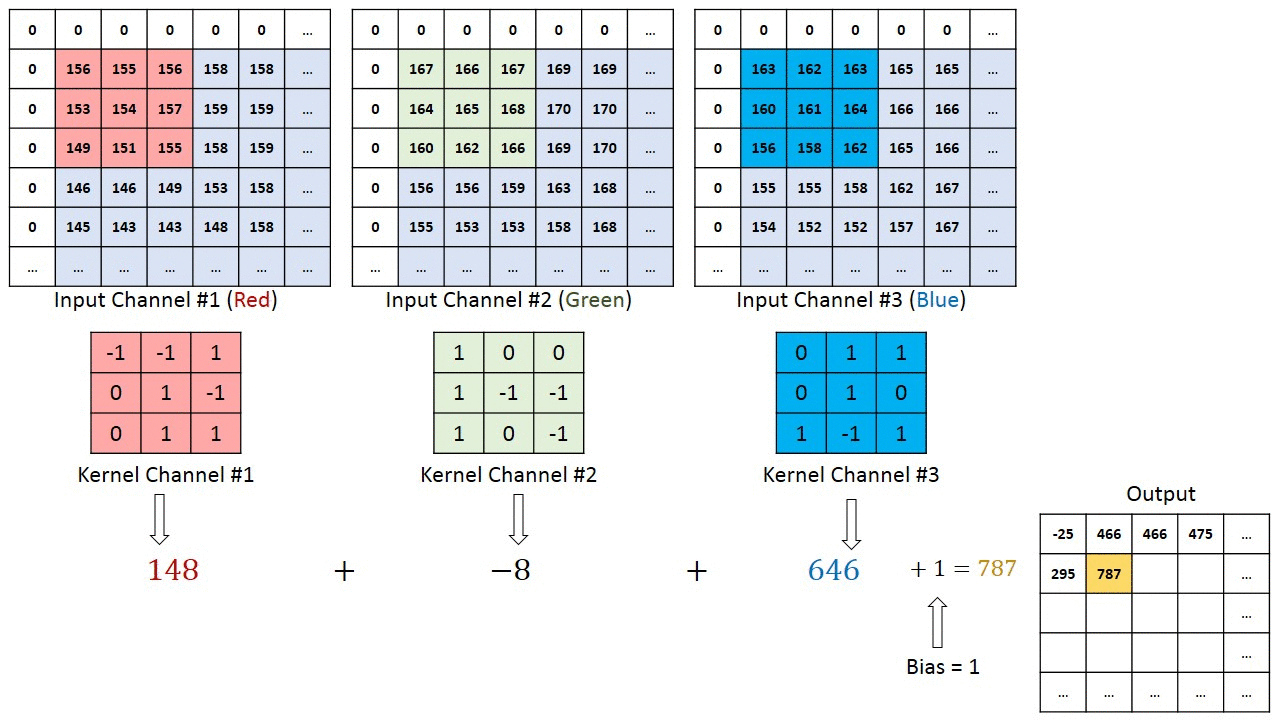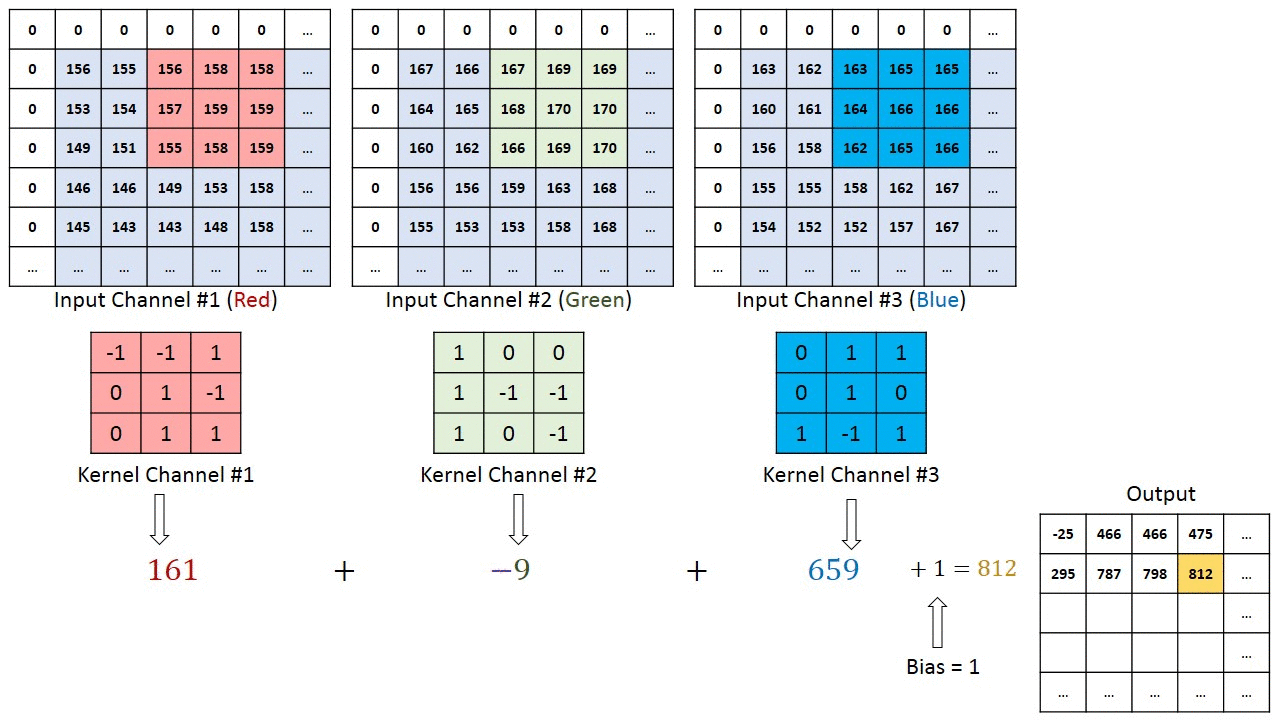
Quando temos 3 canais na figura de entrada, passamos o filtro da convolução em cada kernel e depois somamos os valores dos 3 junto a um viés (bias), salvando o resultado final em UM mapa de características, como na figura a seguir.
Função de Ativação (ReLU)
É usada para adicionar não linearidade no mapa de características. A função de ativação aprimora a dispersão do mapa de características.
Essa função zera todos os valores negativos da saída da camada de convolução.
Camada de Pooling (Subsampling)
O objetivo da camada de Pooling é reduzir a dimensionalidade do mapa de características e aumentar a eficiência computacional, preservando as características mais importantes.
Isso ajuda o modelo a generalizar melhor, previnindo overfitting.
O processo envolve escolher novamente um kernel (matriz de dimensões MxM) que percorrerá o mapa de características advindo da convolução, só que em cada passada escolherá o maior valor entre os que estão na visão da área, de forma que resuma a informação existente ali.
Assim, se um pixel muda de lugar, o mapa será o mesmo.
Existe esse método de escolher o maior (maxpool), mas também o médio (average pool).
Flattening (Achatamento)
O Flatten converte os mapas bidimensionais de características (advindos da última camada de pooling) em um único vetor, ou seja transforma a imagem bidimensional da última camada convolucional em unidimensional. A matriz achatada é usada como entrada da camada totalmente conectada (FC), a qual fará a classificação da imagem.
Camada Totalmente Conectada (Fully-Connected)
Ao final da rede é colocada uma camada Fully connected, onde sua entrada é a saída da camada anterior e sua saída são N neurônios, com N sendo a quantidade de classes do seu modelo para finalizar a classificação.
Relembrando o exemplo do início dessa postagem, se temos que diferenciar bicicletas de motocicletas, então o modelo terá como saída 2 neurônios:
- 0 = classe bicicleta
- 1 = classe motocicleta
Portanto, 2 classes.
Dropout
Essa camada é uma máscara que verifica se os neurônios estão com contribuições significativas durante o treinamento. Se verificarem que não, eles desativam alguns desses neurônios, diminuindo ruído e tornando o treinamento mais eficaz.
_11zon.jpg)
_11zon.jpg)
.png)
0 Comentários